What Financial Software, Martin Fowler, Uncle Bob, & Alexander Hamilton Have in Common -- A Dev’s Take

Written by Leandro, Software developer

As Martin Fowler, software development visionary and writer, once wrote: "A large proportion of the computers in this world manipulate money, so it's always puzzled me that money isn't actually a first class data type in any mainstream programming language."

While this idea comes from his book Patterns of Enterprise Application Architecture (and, full disclosure, I didn’t read it!), he suggests that we use the implementation of a class “Money”, with the attributes “currency” and “amount,” as well as a method called “allocate” that receives a list of proportions and distributes that money without leaking values with rounding. Pretty nifty, I’d say.

In this article, I'll show how we've implemented our own “Money” to solve a real problem of losing cents in apportionments, and we’ll also solve the mystery of this article's title.

We already had a Money class, which made it really easier to write the Money Pattern. So, I’ll start with a hint, it is: DO NOT use Double or Big Decimal to financial values. Build your "Value Object" after having financial values spread all over your system. It'll be harder (but not impossible!) to refactor.

Our Money class doesn't have the attribute currency because we don't have the need for internationalization, at least not yet. And we are not going to implement currency until we actually need it. Just like we didn't have the allocate method until we needed it. So, our Money looked like this:

public class Money implements Serializable {

  private final BigDecimal amount;

  private Money(BigDecimal amount) {
    if (amount == null) {
      throw new AmountCantBeEmptyException();
    }
    this.amount = amount;
  }

  public static Money of(BigDecimal amount) {
    return new Money(amount);
  }

  public Money plus(Money addition) {
    return Money.of(this.amount.add(addition.amount));
  }

  public Money minus(Money discount) {
    return Money.of(this.amount.subtract(discount.amount));
  }

  public Money times(BigDecimal factor) {
    return Money.of(this.amount.multiply(factor));
  }

  public BigDecimal getAmount() {
    return amount;
  }

  @Override
  public boolean equals(Object obj) {
    if (obj == null || !(obj instanceof Money)) {
      return false;
    }
    return this.amount.compareTo(((Money) obj).amount) == 0;
  }

  @Override
  public int hashCode() {
    return this.amount.hashCode();
  }

}

We used this to solve most of our financial problems. Until the day we needed the allocate method. A debt worth $1,000.20 should be apportioned between several accounts with the following rules:

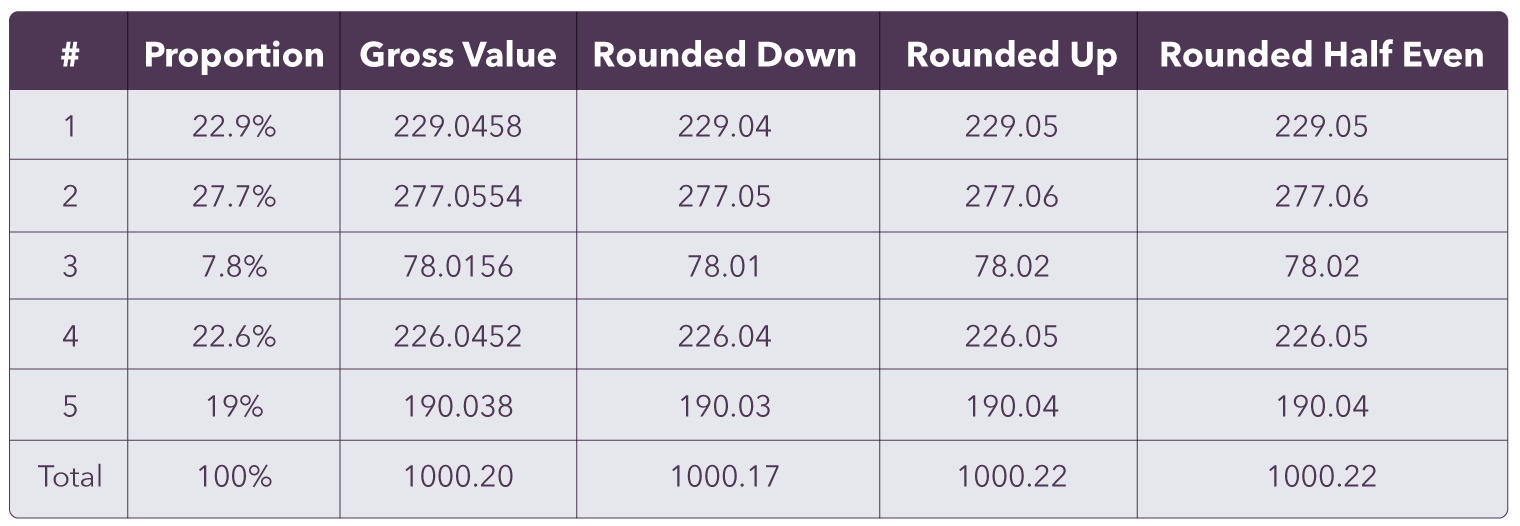
As you can see, applying the apportionment percentage on every item, we'll never get to 1000.20 -- this is because cents are an indivisible unit, so the financial value represented by ‘Money” can't be 229.0458, for example. If we round down, 3 cents are lost in the end. If we round up, we get 2 extra cents. Even using “Round Half Even” we have precision loss.

And guess who faced a problem like this? George Washington himself -- and one of the proposed solutions came from no other than Alexander Hamilton, one of the Founding Fathers, and first United States Secretary of the Treasury. He used the Largest Remainder Method.

The problem faced at that time, described in U.S. Census Bureau, was, in short:

The country had 4 states: each had its own differently-sized population, and 20 Seats in the House of Representatives. How many senators should each state have so they are represented proportionally? A senator, just like a penny, can't be divided into pieces, right? (Just double checking…)

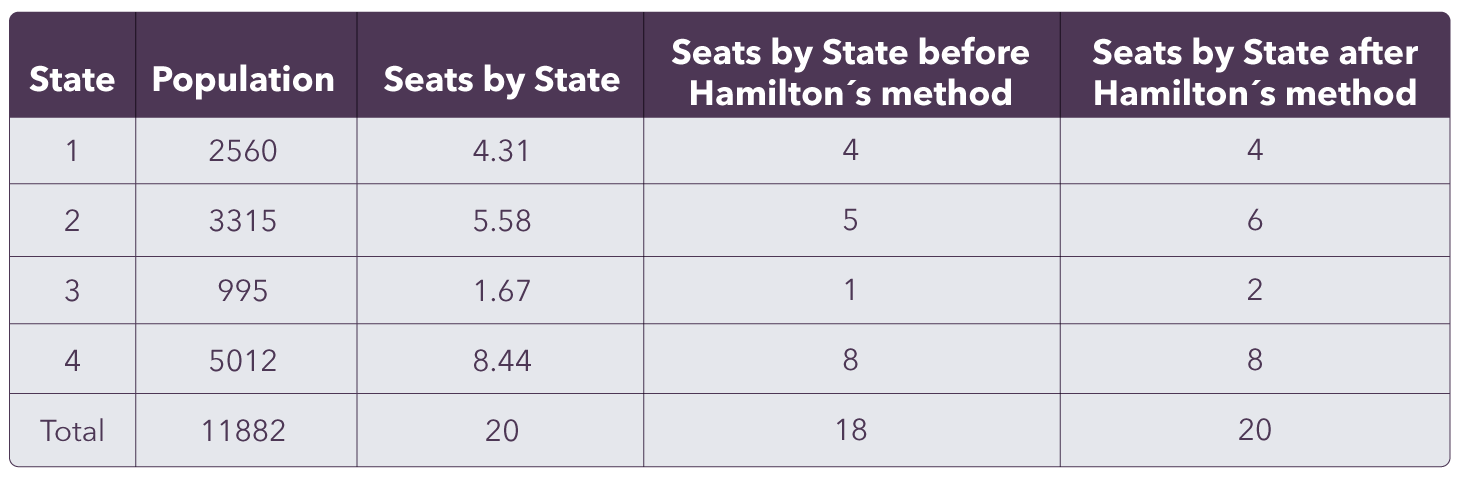
Hamilton's method consists of calculating the proportion between the population of 11882 and the number of seats (20), resulting in the quota of 594.1. Now, for each state, divide its population by the quota. For example: in the state 1, 2560/594.1, getting a quotient of 4.31.

As we have agreed, we can't have 4 senators and 0.31 of a senator for a state. So the number of senators for State 1 is 4, which is the whole part of the result. That happens for every state.

In the end, because of the rounding, the number of senators allocated in the states is 18. So the problem is: to which states should the other 2 senators go?

That's when Hamilton comes with a possible solution. His idea is that we distribute these 2 seats to the states that had the largest decimal part before the rounding. Let me explain.

If we suppress the whole part of the Seats by State column and desc order by the decimal part, we get:

1. 1,67
2. 5,58
3. 8,44
4. 4,31

Since we have a total of 2 seats to redistribute, the states that will receive these senators are the first 2 of the list. Resulting in the column Seats by State after Hamilton's method. Easy, right?

One more thing: there's a paradox to be noticed that was discovered by applying Hamilton's method in the population of Alabama (this is why it’s called the Alabama Paradox.) We won’t cover that here. But this is where Uncle Bob comes in.

Among his countless contributions to the software development community, Uncle Bob spread the SOLID principles. They were relevant in the 90's and they are relevant now. The principle we are focusing is the Open-Closed Principle.

We need to change our Money class to implement the allocate method to distribute its values in ratios without losing any cents. So we created it like:

public class Money implements Serializable {
  private static final BigDecimal ONE_HUNDRED = new BigDecimal(100);

  public List<Money> allocate(List<BigDecimal> ratios, RemainderDistribution distribution) {
    long amountInCents = toCents();
    List<Quota> quotas = new ArrayList<>();
    for (BigDecimal ratio: ratios) {
      quotas.add(new Quota(amountInCents, ratio));
    }
    distribution.distribute(quotas, amountInCents);
    return quotas.stream().map(Quota::toMoney).collect(Collectors.toList());
  }

  public long toCents() {
    return this.amount.multiply(ONE_HUNDRED).longValue();
  }
}

public class Quota {
  private static final BigDecimal ONE_HUNDRED = new BigDecimal(100);

  private long amount;
  private long total;
  private BigDecimal ratio;

  public Quota(long total, BigDecimal ratio) {
    this.total = total;
    this.ratio = ratio;
    this.amount = ratio.multiply(BigDecimal.valueOf(total)).longValue();
  }
}

public interface RemainderDistribution {
  void distribute(List<Quota> quotas, long total);
}

Remember the Alabama Paradox? Even having validated with our Product Manager that we would adopt Hamilton's method, we still have some doubts about how this will behave in the user's hands. So we didn't want to have this fixed in Money class. We wanted to have it changeable whenever needed. In other words, we wanted to make our Value Object Opened for extension but Closed for modification. That's why RemainderDistribution is an interface. One of its possible implementations -- and the one we used -- is HamiltonApportionmentDistribution:

public class HamiltonApportionmentDistribution implements RemainderDistribution {

  @Override
  public void distribute(List<Quota> quotas, long total) {
    long remain = total;
    for (Quota quota : quotas) {
      remain = remain - quota.getAmount();
    }
    List<Quota> sortedQuotas = quotas.stream().sorted(Comparator.comparing(Quota::getFractionalPart).reversed()).collect(Collectors.toList());
    Iterator<Quota> iterator = sortedQuotas.iterator();
    while(remain > 0) {
      remain = remain - 1;
      iterator.next().addRemain(1);
    }
  }

}

This way, we solved that initial problem, where rounding down we lost 3 cents (remember that rounding down is due to the cents, similar to when we round a senator down -- ouch). The calculation must be done using the smallest unit, which in this case is cents. Here is the result:

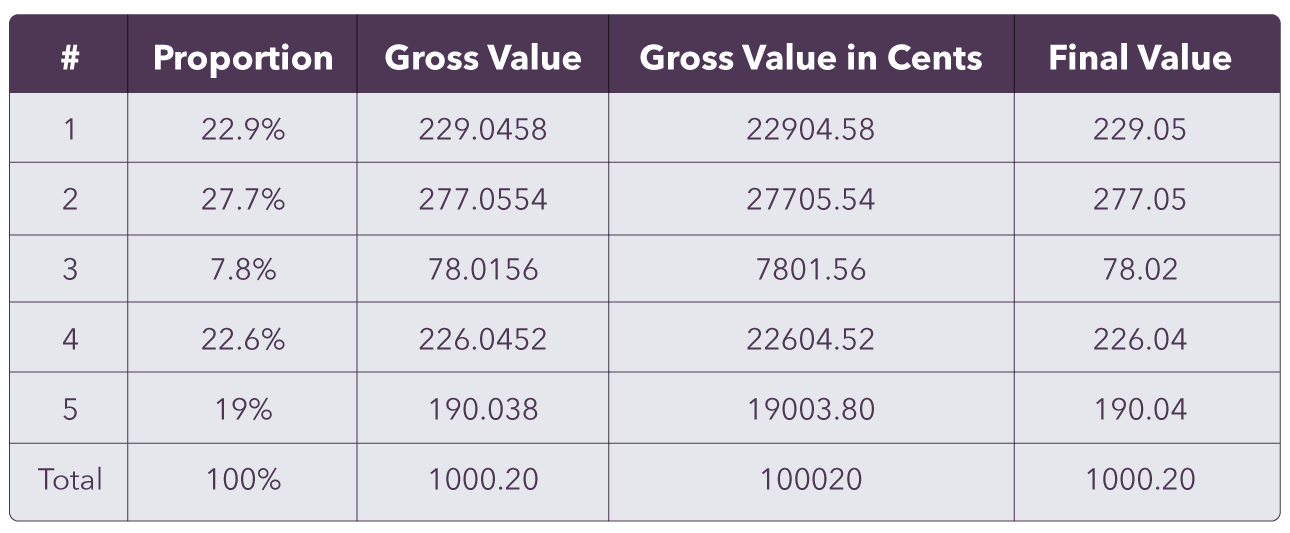
At this point, I hope I have demystified the intersection between Alexander Hamilton, Martin Fowler and Uncle Bob with the Financial System. And, as a bonus, you get some code to apply in your favorite language.

Ah, and for those curious minds, all this code was covered with Unit Tests.

Bonus: if you don't know who Alexander Hamilton was, there is a musical movie available in Disney+, called Hamilton. It tells the story the American First Secretary of Treasury, recorded with rap, hip hop and jazz, directly from Broadway in 2016. Here's the trailer. Enjoy!

--

If you want to stay up to date with all the new content we publish on our blog, share your email and hit the subscribe button.

Also, feel free to browse through the other sections of the blog where you can find many other amazing articles on: Programming, IT, Outsourcing, and even Management.